
Similarly, we will determine the y-derivative considering x as a constant using the chain rule formula.
Solution: First, we will differentiate the composite function f(x, y) = (x 2y 2 + ln x) 3 with respect to x and consider y as a constant. Let us go through an example illustrated below:Įxample: Find the x and y derivatives of the composite function f(x, y) = (x 2y 2 + ln x) 3 While determining the partial derivative of a function with respect to one variable, we consider all remaining variables as constants. We can calculate the partial derivatives of composite functions z = h(x, y) using the chain rule method of differentiation for one variable. Such derivatives are called partial derivatives. Partial Derivatives of Composite Functions in Two VariablesįAQs on Derivatives of Composite Functionsĭerivative of a function in many variables is calculated with respect to one of the variables at a time. What are Derivatives of Composite Functions?ĭerivatives of Composite Functions Formulaĭerivatives of Composite Functions In One Variable
#Fog math calculator how to#
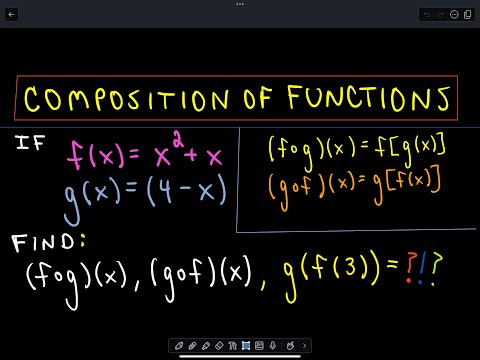
Let us learn how to determine the derivatives of composite functions, the formula to find them, and the concept of partial derivatives of composite functions in two variables with the help of solved examples for a better understanding of the concept. Now, to determine the derivatives of the composite functions, we differentiate the first function with respect to the second function and then differentiate the second function with respect to the variable, i.e., (f o g)'(x) = f'(g(x)).


This implies in a composite function, a function can be substituted into another function and is generally written as (f o g)(x) = f(g(x)). Composite functions are functions when a function is written in terms of another function. Let us first recall the meaning of composite functions. Derivatives of composite functions can be calculated using the chain rule of differentiation.


 0 kommentar(er)
0 kommentar(er)
